边界条件

边界条件表示在边界上的位移和约束，或是应力与面力之间的关系式。

应力边界条件

在$S_σ$部分边界上任意点的应力与边界面上的面力之间的关系式。

应力边界条件的两种表达式

1.在边界点取出一个微分体，考虑其平衡条件，便可得出应力边界条件表达式。
2.在同一边界面上，应力分量应等于对应的面力分量(数值相同 方向一致)由于面力的数值和方向是给定的。 因此,在同一边界面上，应力的数值应等于面力的数值，而面力的方向就是应力的方向，应注意面力和应力正负号不同。

斜面

边界面为斜面的情形，根据微单元体的平衡条件可得，应力(面力)边界条件就是: $$ \left. \begin{array}{l} (lσ_x + mτ_{xy})_s = \overline{f_x} (s) \\ (mσ_y + lτ_{xy})_s = \overline{f_y} (s)\end{array} \right\} (在S_σ上) $$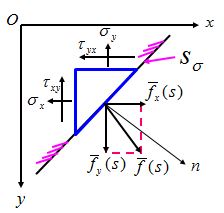

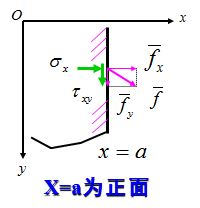
坐标面

边界面为坐标面的情形。
若$x = a $为正$x$面，$(σ_x)_{x=a} = \overline{f_x}$ $\quad$ $(τ_{xy})_{x=a} = \overline{f_y}$
若$x = b $为负$x$面，$(σ_x)_{x=b} = - \overline {f_x}$ $\quad$ $(τ_{xy})_{x=b} = - \overline {f_y}$

位移边界条件

设物体$S_u$边界上给定了$x$ $y$方向的约束位移分量，则该边界上每一点均满足，$(u)_s = \overline u (s) \quad (v)_s = \overline v (s)$ 这就是位移边界条件关系式，对于固定约束边界，$(u)_s = 0 \quad (v)_s = 0$

混合边界条件

物体的一部分具有已知位移，存在位移边界条件，另一部分边界则具有已知面力，存在应力边界条件，这时是混合边界条件。
例如：

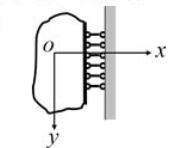
位移边界条件 $x = 0$
应力边界条件 $ (τ_{xy})_s = \overline f_y = 0 $